相对论数学原理,物质告诉空间如何弯曲,空间
来源:应用数学和力学
【在线投稿】
栏目:综合新闻 时间:2022-02-22

这个世界最不可理解的事情是,它竟然是可以理解的。
在二十世纪的头几年里,阿尔伯特·爱因斯坦彻底改变了我们对物理世界的理解。1905年,他提出了狭义相对论,这一理论彻底地破坏了长期存在的关于空间和时间本质的科学和常识假设。例如,同时性:新理论意味着对一个观察者来说发生在同一时间的两件事很可能会在另一个观察者的不同时间发生。从此以后,空间和时间不能再被看作是独立的绝对的量。相反,它们合并了成为一个新的单一实体,称为时空。此外,物质和能量也被结合在一起,形成了物理学中最著名的方程之一:
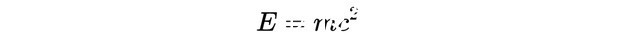
这是激进的理论,但更多的东西还在后面。狭义相对论研究的是在没有引力的情况下物体和光的运动。两百多年来,牛顿的万有引力理论已被证明具有惊人的准确性。它可以精确计算下落的杯子或绕轨道运行的行星的运动。但是,尽管有巨大的实际应用,牛顿的理论与狭义相对论并不兼容(牛顿的引力是瞬时的,而狭义相对论强加了一个自然的速度极限——光速)。
爱因斯坦又花了十年时间来调和引力和狭义相对论,得出了他的广义相对论(于1916年发表)。广义相对论将引力解释为大质量物体附近时空弯曲的效应。它精确地描述了很多现象,如行星轨道的非牛顿偏差、引力时间膨胀、光的引力弯曲和红移。它还被用来预测黑洞的存在和性质,是现代宇宙学的核心——研究宇宙的历史和结构。在适当的条件下,广义相对论可以简化为狭义相对论和牛顿理论。
狭义相对论和广义相对论可以概括如下:
对于所有匀速运动的观察者来说,真空中的光速具有相同的值。质量和能量能弯曲时空。从数学上讲,时空可以用局部平坦的弯曲空间来表示。一个叫作度规的方程描述了这样一个空间的曲率。度规会因区域而异,这取决于空间如何弯曲。光和自由粒子沿着被称为测地线的路径穿越时空,这是由时空的弯曲方式决定的。在适当的情况下,广义相对论应该近似于狭义相对论和牛顿引力。物理定律在所有坐标系中必须具有相同的形式。
或者,更简洁地说,物理学家约翰·阿奇博尔德·惠勒的名言是:
物质告诉空间如何弯曲,空间告诉物质如何运动。
天体物理学家金·格里斯特说:
大多数物理学家都不研究广义相对论,因为它只与牛顿的引力理论不同,与狭义相对论也只是在少数情况下有所不同。但GR(广义相对论)是自然的选择——每当GR不同于牛顿时,GR就被证明是正确的。这就是大自然的运作方式,需要对物理现实进行彻底的反思。
简而言之,相对论是人类理性的胜利,因此值得去了解和掌握。然而,要真正理解这个理论的基础,我们必须解决一些相当有挑战性的数学问题,这就是这个系列将要尝试做的。下面是这个系列将要讨论的关于相对论的数学原理:
介绍必要的基础数学,从基础开始函数的定义,通过微积分和简单的向量,得到第一个度规张量。如果不理解相对论所取代的一些物理学,我不知道如何理解相对论。对牛顿力学进行了简短的讨论,并将更多的时间花在了牛顿的万有引力理论上,我相信这是值得的,其中还包括了如何画出一颗假想行星围绕太阳运行的轨道。讨论狭义相对论和闵可夫斯基时空的奇异世界,包括反直觉的时间膨胀和长度收缩现象。在利用时空图的几何辅助来发展我们的时空知觉之后,我们使用洛伦兹变换来发展一种更代数的方法。最后,我们来看看狭义相对论是如何重新表述力学定律的。简要介绍流形和所有重要的度规张量g_μν的概念。接下是向量和张量,以便让我们更容易理解曲率的数学,包括连接系数、向量的平行传输、测地线和黎曼曲率张量。将这些不同的线索结合在一起,得到爱因斯坦场方程。在这个过程中,我们遇到了等效原理(爱因斯坦最高兴的想法)、时空测地线和能量动量张量。在适当的非相对论条件下,广义相对论方程是如何近似于牛顿力学的公式的。场方程的史瓦西解,这是爱因斯坦场方程的第一个也是最重要的精确解。这个解对缓慢旋转的物体提供了一个很好的近似,如太阳和地球的引力场。我们推导史瓦西解并利用它来讨论广义相对论的四个经典检验。史瓦西解可以用来预测和描述最简单类型的黑洞。对相对论宇宙学的简要介绍。我们从观察到的宇宙的四个关键属性开始,包括宇宙学原理——假设在非常大的尺度上宇宙看起来是一样的。
罗伯逊-沃克度规和弗里德曼方程共同建立了理论框架,使我们能够讨论几个简单的宇宙模型,并对我们自己的宇宙的历史和演化有了深入的了解。请注意,在相对论中,定义速度c等于1通常会使表达变得更简单。例如洛伦兹因子是: