在数学中，希尔伯特空间（以大卫·希尔伯特命名）允许将线性代数和微积分的方法从二维和三维欧几里得空间推广到可能具有无限维数的空间。希尔伯特空间是一个具有内积运算的向量空间，它允许定义距离函数和垂直度（称为正交性）。此外，对于这个距离，希尔伯特空间是完备的，这意味着空间中有足够的限制，可以使用微积分技术。

希尔伯特空间在数学和物理中自然而频繁地出现，典型的是无穷维函数空间。在偏微分方程、量子力学、傅立叶分析（包括信号处理和传热的应用）和遍历理论（形成热力学的数学基础）中，它们是不可或缺的工具。约翰·冯·诺伊曼创造了希尔伯特空间这个术语，用来描述这些不同应用的抽象概念。希尔伯特空间方法的成功开创了一个非常富有成果的泛函分析时代。除了经典的欧几里得空间外，希尔伯特空间的例子还包括平方可积函数空间、序列空间、由广义函数组成的索伯列夫空间和全纯函数的哈代空间。

几何直觉在希尔伯特空间理论的许多方面都起着重要的作用。毕达哥拉斯定理和平行四边形定律在希尔伯特空间中有确切的类比。在更深层次上，在子空间上的垂直投影在优化问题和理论的其他方面起着重要的作用。希尔伯特空间理论是代数、拓扑和几何的融合。

概述

我们已经熟悉代数和几何的融合，即在线性空间R^n中。R^n中的元素可以看作是n维空间中的点，也可以看作是向量。通常，点有坐标，矢量可以相加和缩放。而且，在标准内积存在的情况下，内积由下式给出：

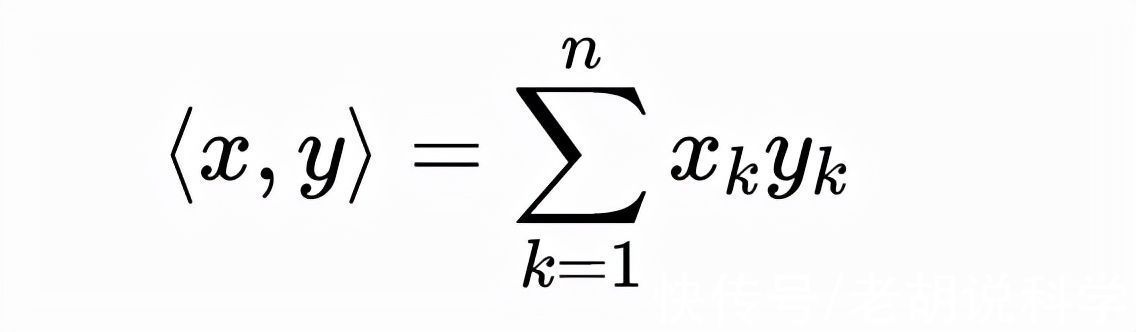
向量的长度是由范数给出的：

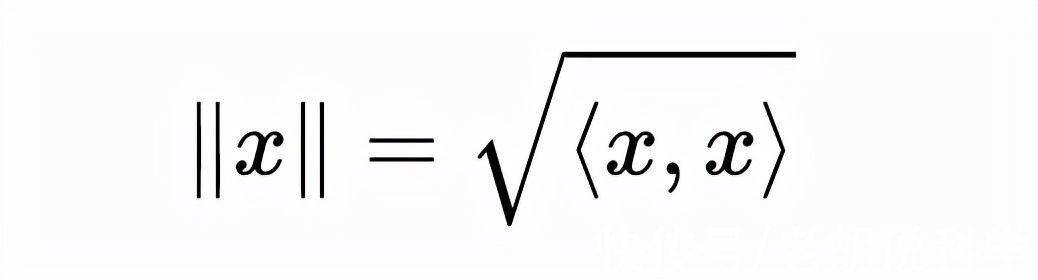
在这个意义上，代数和几何之间的“相互作用”是相当平滑的。不过，只要考虑到无限维线性空间，情况就会发生变化，这也是拓扑学出现的地方。

对于无限维线性空间，所有的线性算子都是连续的，算子的收敛具有单一的含义，任何线性空间都与它的双重对偶自然同构，而且封闭单位球是紧凑的。这些便利条件在无限维的情况下并不存在。虽然基数确实存在，但其存在的证明是非结构性的，而且往往不能明确地给出基数。因此，依靠坐标和矩阵的技术通常是不合适的。线性算子不一定是连续的，事实上，许多感兴趣的线性算子都不是连续的。由两个线性空间之间的所有线性算子组成的空间带有两种不同的拓扑结构，因此也有两种不同的收敛概念。对偶空间的正确概念是所有连续线性算子进入地五十度的空间，即使如此，原空间也只嵌入其双重对偶中。最后，封闭的单位球并不紧凑。

从某种意义上说，希尔伯特空间理论的目的是开发适当的机制，以便能够推理无限维线性空间，并在这些固有的困难和拓扑学的微妙之处加以考虑。因此，研究希尔伯特空间所需的数学背景包括线性代数、拓扑学、公制空间理论和规范空间理论。拓扑群的理论，即群论和拓扑学的融合，也自然而然地产生了。在我们继续阐述这些主题之前，我们先来看看它们中最基本的空间，即实数空间。

实数，一切开始的地方

对于人类观察外部世界来说，最基本的是实数。测量的结果几乎总是被认为是一个实数（至少在某种理想意义上）。这种理想化深深扎根于科学界的传说中，实数的名字就证明了这一点；在所有的数字中，这些都是实数。无论科学对实数的强烈偏好的原因是什么，都是哲学家们的争论。我们只是观察到，无论实数的使用是否合理，实数在科学中的成功是毋庸置疑的。

不过在数学上，实数提出了几个非微不足道的挑战。其中一个挑战是实数的定义，或者换句话说，回答这个问题：什么是实数？对于古希腊人来说，大致上直到毕达哥拉斯派，实数被认为是理所当然的，与我们今天所说的理性数相同。在发现"√2 "是一个无理数之前，这一直是人们普遍持有的信念（这一发现的确切情况尚不清楚）。为实数构建精确的模型需要等待无数个世纪，而超限数的发现和对有多少个实数的理解也是如此。

构造实数

读者很可能对实数有自己的看法。任何对实数的精确解释或说明都属于哲学范畴。从数学角度，我们现在提出一个精确的实数模型的许多构造之一。与任何模型的构建一样，一个人不可能从无到有地构建某些东西。因此，我们假定读者接受有理数（一个模型）的存在，且看法一致，但对实数系统却一无所知。我们将给出实数的精确结构。