问任何一个量子爱好者，什么量子力学的本质？他们首先回答的肯定是薛定谔的猫，接下来呢？可能是薛定谔方程。但是，这个方程究竟是什么，为什么它如此重要，以至于任何一个量子物理学家都会把它记在脑海中？这就是我们将在下面讨论的内容。

所以基本上，薛定谔方程是经典波浪方程的量子力学扩展，给你关于量子力学系统的能量的完整信息。为什么对电子这样的基本粒子使用波浪方程？答案是波粒二象性。

数学

因此，我们从行进波的经典波形方程开始：

其中A是振幅，k=2π/λ=（角）波数，x=位置，ω=角速度，t=时间。

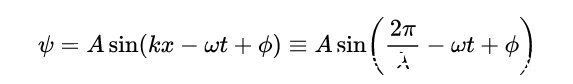
• 古典波浪方程

有些教科书可能会在这个方程中使用余弦函数而不是正弦函数，这与我们所表达的方程是等价的，因为我们是以相对相位计算的。因此，对于φ=90°，我们得到的是余弦函数而不是正弦函数。也就是说，我们可以通过取φ=0°来消除相对相位。

你在文献中可能遇到的这个经典波浪方程的另一种形式是：

这只是我们上面定义的同一个方程，但以欧拉公式的指数形式给出。

• 经典波浪方程的另一种形式，由欧拉公式导出

因此，在我们定义了方程之后，让我们看看当我们将ψ相对于时间（t）和位置（x）进行微分时会发生什么。

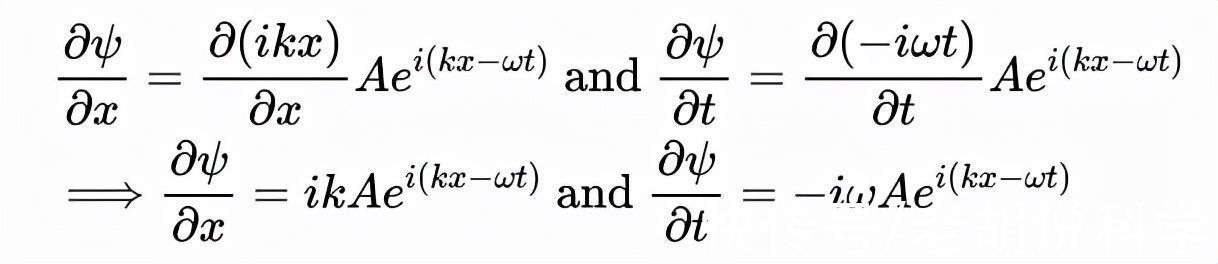
• 将ψ相对于x和t进行微分，可以得到一些已知的表达式

现在，你可能想知道这些方程的好处是什么。但是，仔细一看，我们得出了一些很好的结论。但首先，我们知道，k=2π/λ（λ=波长）。根据德布罗意的关系：

?是缩小的普朗克常数，而p是动量。

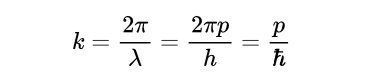
• p和k之间的关系

同样，利用普朗克-爱因斯坦关系，ω=?ω/?=E/?（其中E是能量）。

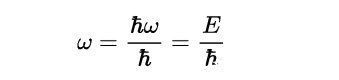
• ω和E之间的关系

在我们的微分经典波方程中使用这两个关系，我们得到：

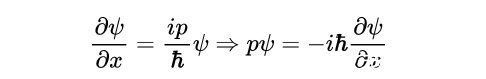
• 动量关系

现在，我们定义量子力学动量算子P-hat，使这个方程在P-hat中成立，即为：

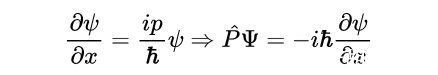
• 动量算子。请注意，psi的符号由小到大的变化是为了表示从经典到量子的视角变化。

同样，对于能量，我们将能量算子定义为：

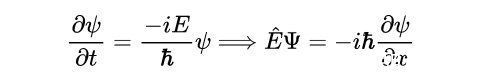
• 能量关系。这里发生了一个类似的从经典到量子的视角变化。

现在，我们从经典力学知道，动能（E）=p^2/2m。利用这个关系，我们得到：

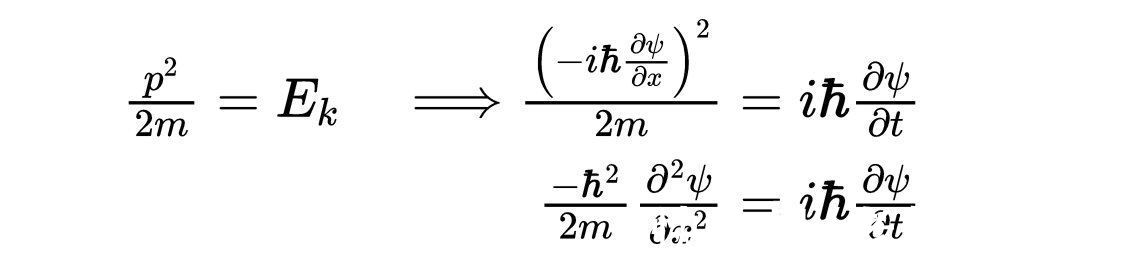
• 一维的时间相关薛定谔方程。

简化后的数学得到了上式方程中的下面一个。这个方程被称为一维的随时间变化的薛定谔方程。

在这个问题上增加更多的维度，我们得到方程的一般形式。

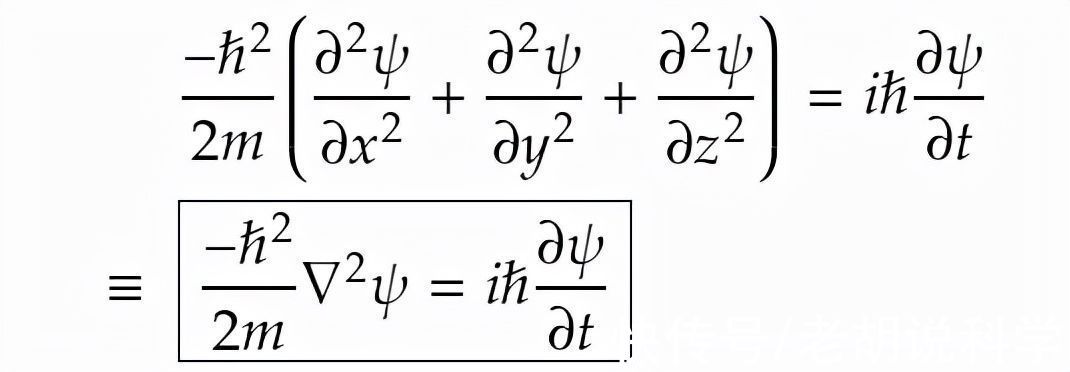
三维的时间相关性薛定谔方程。（倒三角平方）函数被称为拉普拉斯或拉普拉斯算子。

完善方程

在上面给出的方程中，你可能会注意到一件事，那就是所有的起始方程，都是从经典力学中继承下来的，是对应于物体的动能的。而且那是真的。我们还没有在这些方程中加入物体的势能。让我们来做吧。

我们把量子系统的势能定义为势能算子V，并在三维空间中把它数学地写成V（x，y，z，t）ψ（x，y，z，t）。

因此，完整的能量方程是由：

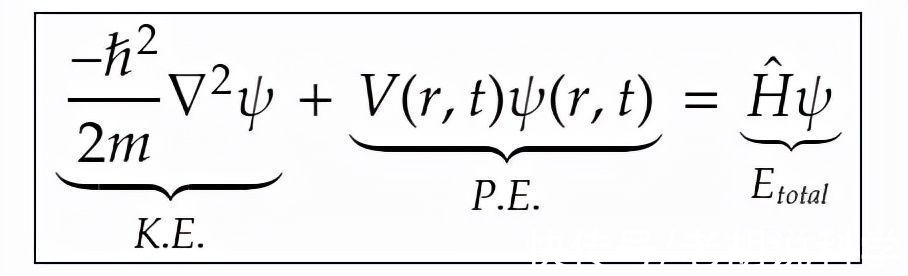
• 三维中完整的时间相关型薛定谔方程。请注意，r被用来作为三个空间维度的速记表示。还请注意，量子系统的总能量被称为系统的哈密尔顿，它给你量子系统的总能量。

与时间无关和与空间无关的方程式

那么，上面我们铺垫了相当多的数学知识。如果φ不依赖于空间和时间，这将是它的最终形式。